Gross Margin (gross profit) is how much your firm earned this year by making
bikes and selling them.
Gross Margin = (Sales Units x Average Wholesale Price) – (Sales Units x Average Unit Cost)
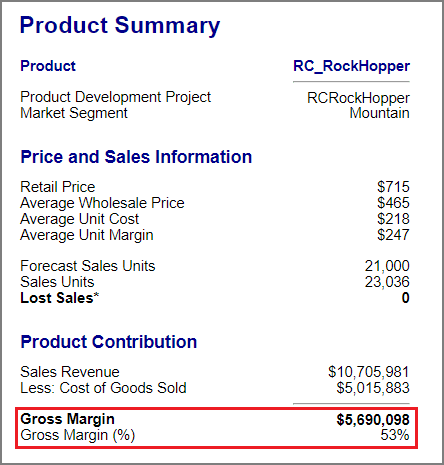
Your firm may also use Gross Margins to determine how much money you have left over from sales to cover other operating expenses.
The Gross Margin amount does not include the following costs: Inventory Costs, Product Marketing costs, and Product Development costs.
What if I have a negative Gross Margin?
A negative Gross Margin means that your per unit costs are higher than your wholesale price and that your product is running at a loss.
There are three things that you can do to increase your Gross Margins:
- Increase your prices
- Reduce your retailer margins
- Develop your product(s) to reduce their manufacturing costs.
Keep in mind that extreme changes to the above may have a negative effect on your Gross Margins.
This support article applies to the following simulations:
MikesBikes Introduction to Business Simulation
MikesBikes Advanced Strategic Management Simulation
Music2Go Marketing Simulation
AdSim Advertising Simulation